BİRİNCİ DERECEDEN İKİ BİLİNMEYENLİ DENKLEM SİSTEMİ
a, b, c Î
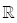 , a ¹ 0 ve b ¹ 0 olmak üzere,
, a ¹ 0 ve b ¹ 0 olmak üzere,
ax + by + c = 0 denklemine birinci dereceden iki bilinmeyenli denklem denir.
Bu denklem düzlemde bir doğru belirtir. Doğru üzerindeki bütün noktaların oluşturduğu ikililer denklemin çözüm kümesidir.
Buna göre, ax + by + c = 0 denkleminin çözüm kümesi birçok ikiliden oluşur.
a, b, c Î
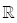 olmak üzere,
olmak üzere,
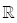 [SUP]2[/SUP] için sağlanıyorsa
[SUP]2[/SUP] için sağlanıyorsa
Birden fazla iki bilinmeyenli denklemden oluşan sisteme birinci dereceden iki bilinmeyenli denklem sistemi denir.
Çözüm Kümesinin Bulunması
Birinci dereceden iki bilinmeyenli denklem sistemlerinin çözüm kümesi; yok etme yöntemi, yerine koyma yöntemi, karşılaştırma yöntemi, grafik yöntemi, determinant yöntemi gibi yöntemlerden biri ile yapılır.
Biz burada üçünü vereceğiz.a. Yok Etme Yöntemi: Değişkenlerden biri yok edilecek biçimde verilen denklem sistemi düzenlenir ve taraf tarafa toplanır.
Taraf tarafa toplandığında veya çıkarıldığında (ya da bir düzenlemeden sonra) değişkenlerden biri sadeleşiyorsa “Yok etme yöntemi” kolaylık sağlar.
b. Yerine Koyma Yöntemi: Verilen denklemlerin birinden, değişkenlerden biri çekilip diğer denklemde yerine yazılarak sonuca gidilir.
Denklemlerin birinden, değişkenlerden biri kolayca çekilebiliyorsa, “Yerine koyma yöntemi” kolaylık sağlar.
c. Karşılaştırma Yöntemi: Verilen denklemlerin ikisinden de aynı değişken çekilir. Denklemlerin diğer tarafları karşılaştırılır (eşitlenir).
Her iki denklemden de aynı değişken kolayca çekilebiliyorsa, “Karşılaştırma yöntemi” kolaylık sağlar.
ax + by + c = 0
dx + ey + f = 0
denklem sistemini göz önüne alalım:
Bu iki denklemin her birinin düzlemde bir doğru belirttiği göz önüne alınırsa üç durum olduğu görülür.
Birinci durum:
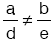
Bu durumda, verilen denklem sisteminin çözüm kümesi bir tek noktadan oluşur.
İkinci durum:ise, bu iki doğru çakışıktır.
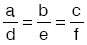
Doğru üzerindeki her nokta denklem sistemini sağlar.
Bu durumda, verilen denklem sisteminin çözüm kümesi sonsuz noktadan oluşur.
Üçüncü durum:ise, bu iki doğru paraleldir.
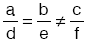
Denklem sistemini sağlayan hiçbir nokta bulunamaz.
Bu durumda, verilen denklem sisteminin çözüm kümesi boş kümedir
a, b, c Î
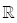
ax + by + c = 0 denklemine birinci dereceden iki bilinmeyenli denklem denir.
Bu denklem düzlemde bir doğru belirtir. Doğru üzerindeki bütün noktaların oluşturduğu ikililer denklemin çözüm kümesidir.
Buna göre, ax + by + c = 0 denkleminin çözüm kümesi birçok ikiliden oluşur.
a, b, c Î
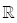
ax + by + c = 0
denklemi her (x, y) Î
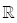
a = b = c = 0 dır.
Birden fazla iki bilinmeyenli denklemden oluşan sisteme birinci dereceden iki bilinmeyenli denklem sistemi denir.
Çözüm Kümesinin Bulunması
Birinci dereceden iki bilinmeyenli denklem sistemlerinin çözüm kümesi; yok etme yöntemi, yerine koyma yöntemi, karşılaştırma yöntemi, grafik yöntemi, determinant yöntemi gibi yöntemlerden biri ile yapılır.
Biz burada üçünü vereceğiz.a. Yok Etme Yöntemi: Değişkenlerden biri yok edilecek biçimde verilen denklem sistemi düzenlenir ve taraf tarafa toplanır.
Taraf tarafa toplandığında veya çıkarıldığında (ya da bir düzenlemeden sonra) değişkenlerden biri sadeleşiyorsa “Yok etme yöntemi” kolaylık sağlar.
b. Yerine Koyma Yöntemi: Verilen denklemlerin birinden, değişkenlerden biri çekilip diğer denklemde yerine yazılarak sonuca gidilir.
Denklemlerin birinden, değişkenlerden biri kolayca çekilebiliyorsa, “Yerine koyma yöntemi” kolaylık sağlar.
c. Karşılaştırma Yöntemi: Verilen denklemlerin ikisinden de aynı değişken çekilir. Denklemlerin diğer tarafları karşılaştırılır (eşitlenir).
Her iki denklemden de aynı değişken kolayca çekilebiliyorsa, “Karşılaştırma yöntemi” kolaylık sağlar.
ax + by + c = 0
dx + ey + f = 0
denklem sistemini göz önüne alalım:
Bu iki denklemin her birinin düzlemde bir doğru belirttiği göz önüne alınırsa üç durum olduğu görülür.
ax + by + c = 0
dx + ey + f = 0
denklem sisteminde,ise, bu iki doğru tek bir noktada kesişir.Birinci durum:
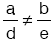
Bu durumda, verilen denklem sisteminin çözüm kümesi bir tek noktadan oluşur.
İkinci durum:ise, bu iki doğru çakışıktır.
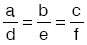
Doğru üzerindeki her nokta denklem sistemini sağlar.
Bu durumda, verilen denklem sisteminin çözüm kümesi sonsuz noktadan oluşur.
Üçüncü durum:ise, bu iki doğru paraleldir.
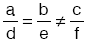
Denklem sistemini sağlayan hiçbir nokta bulunamaz.
Bu durumda, verilen denklem sisteminin çözüm kümesi boş kümedir
Moderatörün son düzenlenenleri: